Army Strength Scales Non-Linearly: 1+1=3

Armies are greater than the sum of their parts:

2 Dragoons go even against 2 Dragoons.

4 Dragoons will beat 2 Dragoons twice and then some.

An army that is twice as powerful as its opposition — whether due to size, unit upgrades, General/Patriot buffs or something else — can deal with a half-strength army more than twice. An army that is ten times as powerful (think Machine Guns vs Crossbows or something) can face the tenth-strength army a near-infinite amount of times in practical terms.

The application of an army’s power against an opposing force does not scale linearly with the army’s apparent power. Whenever you increase an army’s strength, you increase its fighting capability by more than what you added. Army strength increases non-linearly.

This simple concept is one of the most important aspects of successful combat in RoN, and is applicable to both symmetrical and asymmetrical fights.

 

Update (June 2019):

I’ve discovered that this concept has actually been described in real-world combat by Frederick Lanchester and M. Osipov, and it’s known as Lanchester’s Law – or more specifically in this case, Lanchester’s Square Law. It doesn’t translate 1:1 into RTS games (although it seems quite a few people have applied it in StarCraft), but it’s cool to see that I independently figured out actual military strategy as it applies to Rise of Nations.

Original article follows.

 

Let’s look into why this is the case by simplifying every unit into two things: damage output (i.e. DPS) and durability (i.e. DPS absorbed before death). Units contribute their damage output to a fight so long as they stay alive, which is defined by their durability. A high damage unit that dies the instant a fight breaks out is of little value since they have not stayed alive long enough to contribute their high damage. On the other extreme, an invulnerable Citizen (which we’ll pretend can’t become a Militia etc) is almost worthless in a fight. Even though they live forever, their damage output is so insignificant that their durability is irrelevant, and their total contribution may as well be a rounding error.

To further quantify these examples, let’s add some numerical values. Let’s say that 1 point of durability means it takes 1 second of 1 DPS to get to 0 health (which mean 10 DPS removes 10 durability per second). Consider the following:

1. Billy the Bazooka has 40 DPS but is at 10 durability (perhaps because he’s near-lethally wounded already).
2. Danny the Dragoon has 20 DPS and 100 durability.
3. Sammy the Invulnerable Citizen has 1 DPS but infinite durability.

Let’s say that each of our friends gets into a fight against an enemy City. The City will have 10 DPS and the fight will last for 20 seconds. Under these circumstances, each of our friend’s total damage contributions can be simplified into the following:

1. Billy the Bazooka dies immediately. 40 DPS * (10 durability / 10 DPS from the enemy City (which is 1 second of survival)) = 40 total damage contribution.
2. Danny the Dragoon dies halfway into the fight. 20 DPS * (100 durability / 10 DPS from the enemy city (which is 10 seconds of survival)) = 200 total damage contribution.
3. Sammy the Invulnerable Citizen naturally doesn’t die. 1 DPS * (20 seconds) = 20 total damage contribution.

Doubling the DPS of any of these three units will double their damage contribution. However, keeping their DPS the same but then adding a second identical unit will triple the combined damage contribution of the two units (except for Sammy, because the rules don’t apply the same way when you’re invulnerable).

Let’s revisit the real-world example used in the introduction: Dragoons.

A Super-Dragoon with 4x damage and 4x durability can contribute 16 times as much total damage as a normal Dragoon.

While 4 normal Dragoons also start with 4x total damage and 4x total durability, they also have 4 distinct lives, and each time one of them dies, the effective DPS of the dead Dragoon becomes zero. If defining the power of these Dragoons by the number of single Dragoons they can fight against, they’re only ~10x as powerful, not 16x as powerful (it takes ~10 solo Dragoons to kill the 4 Dragoons – so long as the solo Dragoons shoot the same target when possible).

Of course, “Dragoon” can be replaced with another unit and the outcome will be essentially the same.¹ While this overall concept is much simpler to explain using a single unit, real armies in the field consist of a number of different units. That’s where the application is the most complex, but also the most valuable.

Anecdote: Alexander the Great Campaign

A great example of non-linear army strength scaling in action happened while I was playing the Alexander the Great campaign on Toughest, and what happened repeatedly during that campaign was actually the inspiration for writing this article.

In order to win some of the toughest (haha) battles in that campaign at max difficulty, you have to do a lot of work. Based on my experience, I believe you need:

• A massive army. If you’re not hitting the maximum pop cap, you probably can’t win within the timer.
• This massive army to be made of the right units. If your army composition is too far out of balance, this will cause you to lose (due heavily to the strength of War Elephants grr).
• Constant reinforcements for your massive army. Your army will have a very high turnover out of necessity, because your troops are going to inevitably be dying by the masses. You need to be constantly replenishing your ranks to counteract this, otherwise you’ll get outnumbered after your initial salvo.
• Reinforcements produced close to the frontline. The further your unit production buildings are from the action, the more time your reinforcements spend simply reaching the fight. Every unit not in combat is a unit that is just that – not in combat. Units not in combat do not contribute to the current strength of your army in a fight.
• A robust (read: maxed out) economy to support infinite production from multiple sets of unit producing buildings. If you only have a couple Barracks and couple Stables, you won’t be able to build replacement troops fast enough. On the most difficult mission of the campaign (at least on my play-through), I found 5 Barracks / 5 Stables on infinite queue next to the frontline to be inadequate, and didn’t manage to win the fight enough to push forward until I built a number of additional structures also on infinite queue.

Despite initially satisfying all these factors when engaging, I was somehow still losing some of my extended fights. I already had the maximum economy cap, so increasing unit production wasn’t a sustainable option. To win from this position, I had to pull back the handful of surviving troops about a screen, wait a few minutes to once again hit the pop-cap, then re-engage.

It was slow going, but with the above points combined with better application of non-linear army strength scaling, I was able to win that mission.

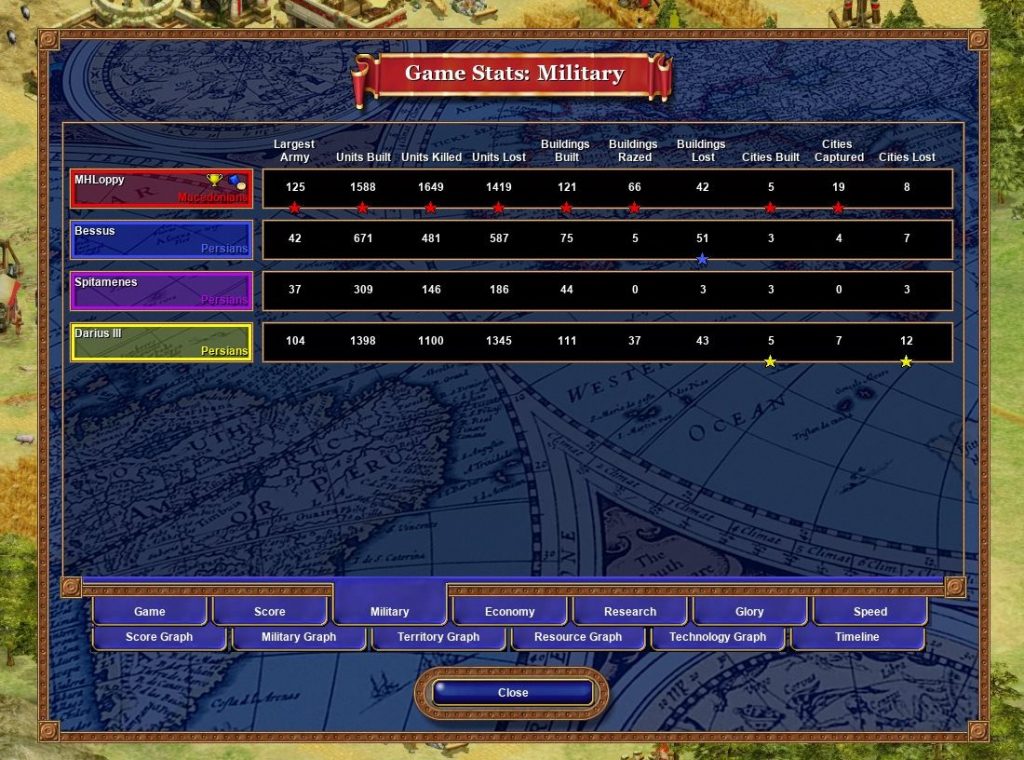
What I had neglected was that my troops were dying slightly slower than I could replenish them whenever I pushed a heavily fortified position. After fighting for a few minutes non-stop, my army would not be at pop-cap despite building as many infinite-queue-reinforcements as I thought feasible. That meant that the defending force (which was also being constantly reinforced) had the upper hand, and all I was doing was voluntarily slaughtering my own troops against a stronger army. Sometimes having “only” 100 troops is actually not enough.

Picking Winning Fights

Let’s hop back to “real” games. Unlike in the Alexander campaign, infinite-queue slugfests lasting an hour or more are not the norm.

Because of the non-linear nature of army strength scaling, it’s extra-important to pick winning fights and avoid losing ones – at least until you can reinforce / upgrade / otherwise improve your odds. As demonstrated in the 4 vs 2 Dragoons example, when you pick advantageous fights you incur fewer losses than your opponent, and can therefore expend less resources when repopulating your troops.

It’s usually better in the long run to give up some ground temporarily than it is to force a losing fight. There are a few exceptions (e.g. you usually want to hold your capital more aggressively), but replacing an entire army when you lose a fight is often debilitatingly expensive – and given that you lost the fight, you probably need to build even more units than you originally did if you want to have a chance of winning the next time you scuffle with your opponent.

By picking a winning fight, you spend less on replacement troops, allowing you to expand your army even further (and compound your advantage), or simply spend the resources elsewhere.

Home Ground Advantage

In RoN, the defending army nearly always has the advantage.

Even if you discount territory, terrain, and any cities or defensive structures, this advantage remains – because it stems heavily from having unit production buildings closer to the front.

Once again: troops that are in transit are not in combat, and will not contribute to the fight until they are.

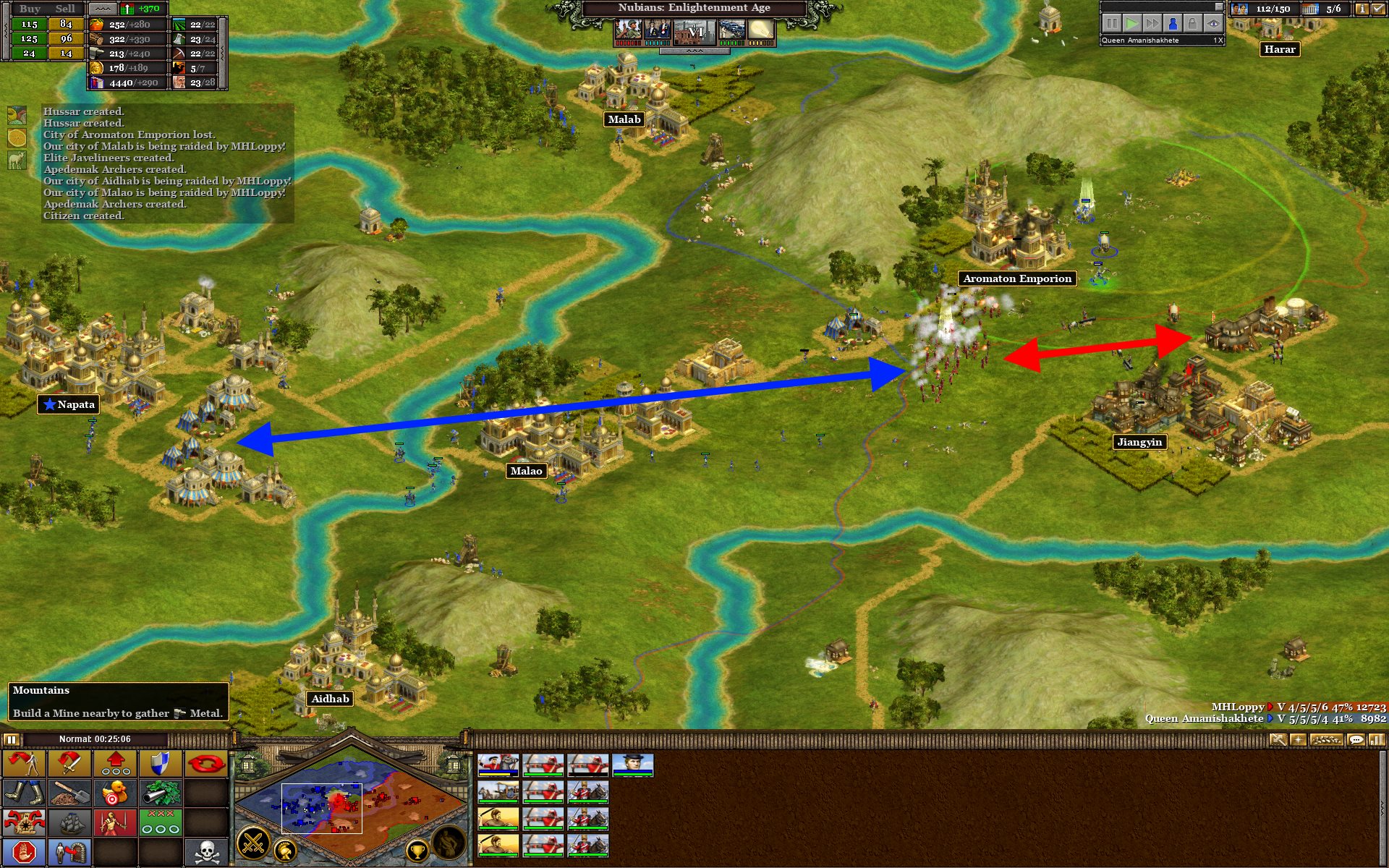
While the defender will always retain some of this advantage (you can’t build in their territory), you can negate much of it by building your production buildings close to the frontline. In the screenshot above my opponent actually has a lone Barracks next to the frontline, he just wasn’t building from it. If he had plopped down a Stable there and then used those buildings instead of the ones at his capital, I likely would’ve lost the initial fight and never gotten to the position shown.

Having your reinforcements spend less time in transit bolsters the number of troops you have available for immediate combat at any given moment at your frontline, which better leverages non-linear scaling.

Summary

• Army strength scales non-linearly; an army is greater than the sum of its parts.
• The more powerful an army is versus an opposing force, the less losses it will incur when fighting that force. This in turn makes it important to pick advantageous fights and avoid disadvantageous fights when possible – this will allow you to spend less resources on army maintenance.
• Reinforce your army before and during fights if resources allow, and reduce the transit time for reinforcements to reach the frontlines.

 

---

 

1. There’s a small variance in regards to unit targeting (over-killing a unit wastes damage, for example), but for the most part it’ll be consistent.